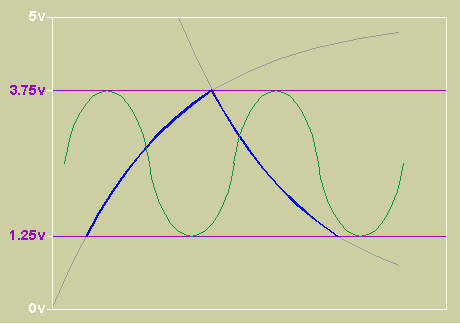
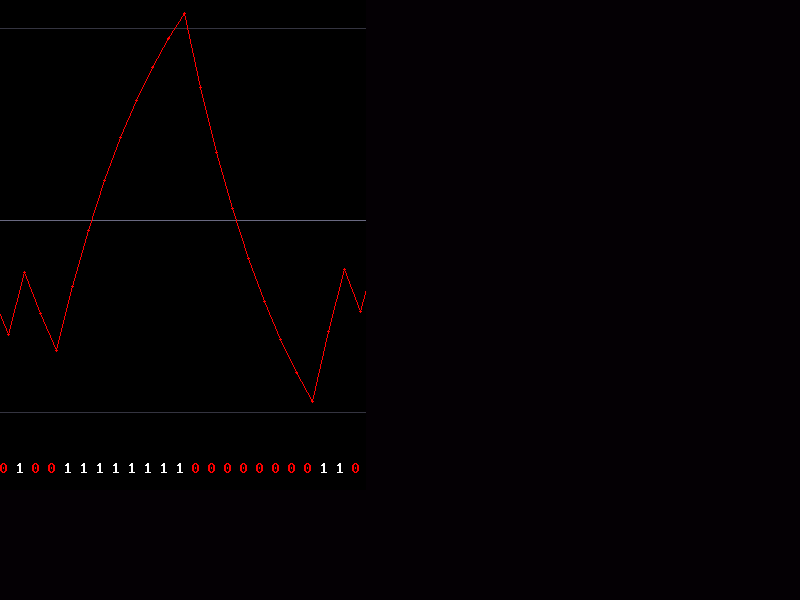This may be seen more clearly in the waveform window of my BTc Encoder program below;
The 2 lines marked with purple arrows are the 1.25v and 3.75v lines as in the example above. The yellow waveform is the original 8 bit waveform and fits totally within the lines at all times. The red wave is the BTc encoded waveform. You can see it is free to exceed the voltage limits that always constrain the orig waveform.

Reactive or Predictive?
In my 2001 BTc Encoder I tested both encoding methods;
Reactive is where the encoder produces ONE new value for each sample. It reacts to the change in the orig waveform. If the BTc waveform is less than the new sample it produces a 1 bit, if the BTc wave is currently above the new sample, it produces a 0 bit. Reactive is the system used by most encoding processes in the real world, it is faster and simpler to encode.
Predictive is a system that generates TWO possible outcomes for each new sample. Then the two outcomes are compared to the desired sample and the BEST outcome (ie the closest to the desired sample) is chosen.
I settled on the Predictive system for my 2001 BTc Encoder and have used it since. The predictive system generates better sound quality; it produces the closest result to the desired waveform and responds instantly to the new sample. The reactive system lags behind the desired waveform, doing the best it can to stay close to it after it changes. I chose the predictive system because it has slightly better sound quality. If you are using a PIC or other micro to do real-time encoding you may wish to use reactive encoding to sacrifice a little quality but reduce the processing required.
The following examples of my BTc encoding algorithm are written as simple "psuedo code" so they can be easily adapted to whatever language (or micro) you program with.
newsample (0-255) is the next sample from the wave file we are encoding
lastbtc (0-255) is the existing position (last known position) of the BTc waveform
newbit (0-1) is the result of the BTc encoding
Reactive BTc algorithm
Assuming 8-bit wave file, 8-bit math and BTc4 encoding;
// Scale the next wave sample and place in centre
newsample = (newsample / 2) + 64;
// generate the BTc bit,
// does the BTc wave need to react UP or DOWN to follow it?
if(newsample > lastbtc)
{
newbit = 1; // BTc must move UP
dist = (256 - lastbtc); // calc total distance to charge
dist = (dist / 4); // BTc4, only charge 1/4 distance
lastbtc = (lastbtc + dist); // where it charges up to
goto done;
}
else
{
newbit = 0; // BTc must move DOWN
dist = lastbtc; // calc total distance to charge
dist = (dist / 4); // BTc4, only charge 1/4 distance
lastbtc = (lastbtc - dist); // where it charges down to
goto done;
}
Predictive BTc algorithm
Also using an 8-bit wave, 8-bit math and BTc4. Basically this is how my BTc Encoder software does it;
// Scale the next wave sample and place in centre
newsample = (newsample / 2) + 64;
// generate a "1" (high) outcome
dist = (256 - lastbtc); // calc total distance to charge
dist = (dist / 4); // BTc4, only charge 1/4 distance
highbtc = (lastbtc + dist); // where it charges up to
// generate a "0" (low) outcome
dist = lastbtc; // calc total distance to charge
dist = (dist / 4); // BTc4, only charge 1/4 distance
lowbtc = (lastbtc - dist); // where it charges down to
// calc distance from high outcome (up or down) to new sample
if(highbtc > newsample) disthigh = (highbtc - newsample);
else disthigh = (newsample - highbtc);
// calc distance from low outcome (up or down) to new sample
if(lowbtc > newsample) distlow = (lowbtc - newsample);
else distlow = (newsample - lowbtc);
// see which outcome is closest to new sample and generate the bit
if(disthigh > distlow) // low is closest
{
newbit=0;
lastbtc = lowbtc;
}
else // else high is closest
{
newbit=1;
lastbtc = highbtc;
}
goto done;
There are some optimisations that can be done to shrink the above code examples but I have left them long for clarity. You can see the predictive algorithm takes roughly twice as long but will still fit in a handful of PIC assembler instructions. Unlike floating point math, the whole algorithm only requires 8-bit add and subtract and /2 /4 etc (right shift). It encodes the waveform VERY quickly!
TalkBotBrain Project!

Support the TalkBotBrain project! This neat PCB is sold fully assembled and pre-programmed and plays 1bit BTc sound from its 1 Megabit of eeprom memory and built in amplifier. You can load any sounds you like into it with a serial lead. It has open-source-firmware and the TalkBot is sold as a reduced-cost product to actively promote talking technology. Buy a TalkBot and make something talk!
www.TalkBotBrain.com
The encoding algorithms;
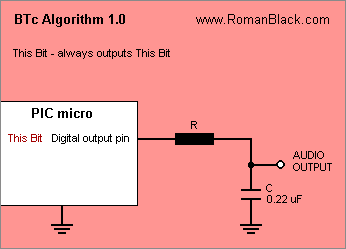
Algorithm BTc 1.0
Playback.
This is as simple as it gets. Each new bit is read from the BTc sound data. It is output on a digital output pin. That pin is connected to a RC low-pass filter. The filter output is the audio output. This is the "traditional" way to play 1bit sound and has been used for decades.
Encoding.
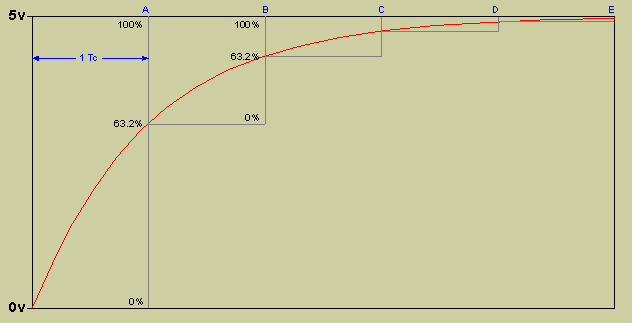
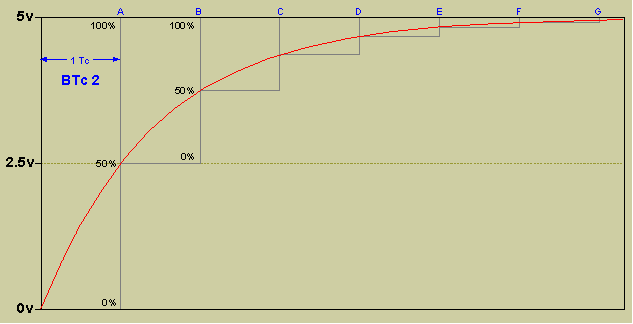
My original BTc1.0 algorithm of 2001 allows the RC filter to be mathematically modeled very easily. Using a Binary Time Consant of 8 (or BTc8) we have chosen a resistor and capacitor value so that for every sound sample (Tc) the voltage on the capactor rises or falls 1/8 of the distance to Vcc or Gnd.
The original audio waveform has been scaled to fit entirely in the area from 1/4 of Vcc to 3/4 of Vcc so the RC slope is slightly more linear, and there is some room to overshoot.
Encoding is a process where an audio wave file is "encoded" to 1bit BTc format, so each sample in the wave file becomes 1 bit, either a 1 or a 0.
a1.0 Encoding Example (using BTc8);
variables; NewSample = the new audio sample, scaled to 1/4-3/4 Vcc range LastVoltage = the cap voltage (audio output) from the last bit NewVoltage = the cap voltage (audio output) after we encode this new bit NewBit = the newly encoded BTc bit encoding; 1. generate a 1bit; distance = (Vcc - LastVoltage) / 8 Voltage1 = LastVoltage + distance 2. generate a 0bit; distance = (LastVoltage - Gnd) / 8 Voltage0 = LastVoltage - distance 3. Find which bit is closest to the desired audio sample; if Voltage1 is closest to NewSample then; NewBit =1, and NewVoltage = Voltage1 if Voltage0 is closest to NewSample then; NewBit =0, and NewVoltage = Voltage0 4. Save the cap voltage and repeat for the next audio sample; LastVoltage = NewVoltage Repeat
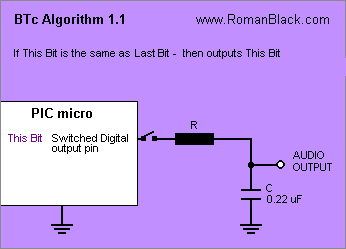
Algorithm BTc 1.1 (new for BTc Encoder v3.0)
This was one of my original encoding and playback algorithms of 2001, but was never included in any of the BTc Sound Encoders until now as it performs very poorly. However people keep mentioning this system to me as it seems like a logical algorithm and on first thought people think it will perform well. Now I have supported it in BTc Sound Encoder v3.0 you can see its problems for yourself and use it if you find it suitable for anything.
Playback.
The new bit is read from the BTc sound data. It is compared with the last bit. If the 2 bits are the same the new bit is output on the digital output pin. If the new bit is different from the last bit the digital output pin goes high-impedance (disconnects). The resistor value is R.
The result is that for two successive 1 bits the cap voltage rises, and for two successive 0 bits the cap voltage falls. But where the bits are fluctuating the cap voltage stays the same, causing (in theory) less output ripple and a better playback quality.
a1.1 Encoding Example (using BTc8);
variables; NewSample = the new audio sample, scaled to 1/4-3/4 Vcc range LastVoltage = the cap voltage (audio output) from the last bit NewVoltage = the cap voltage (audio output) after we encode this new bit LastBit = the encoded bit from last time NewBit = the newly encoded BTc bit encoding; 1. generate a 1bit; distance = (Vcc - LastVoltage) / 8 Voltage1 = LastVoltage + distance 2. generate a 0bit; distance = (LastVoltage - Gnd) / 8 Voltage0 = LastVoltage - distance 3. voltage won't change if the last bit was different, so; if LastBit was 1; Voltage0 = LastVoltage if LastBit was 0; Voltage1 = LastVoltage 3. Find which bit is closest to the desired audio sample; if Voltage1 is closest to NewSample then; NewBit =1, and NewVoltage = Voltage1 if Voltage0 is closest to NewSample then; NewBit =0, and NewVoltage = Voltage0 4. Save the cap voltage and repeat for the next audio sample; LastVoltage = NewVoltage Repeat
Technical issues with algorithm 1.1 What seems like a good way to smooth the 1bit output actually performs badly for a few reasons; 1. where algortihm 1.0 typically has its noise artifacts at bitrate/2 and bitrate/3 (first and second harmonics) these are high frequency and easy to filter out, but algorithm 1.1 responds slower and the noise component of the sound is often at bitrate/5 or even much worse. This is a much lower frequency hence harder to filter and more annoying to the ear. 2. The slower response of algorithm 1.1 means that it must often overcompensate to reach the target, giving a larger amplitude noise component. 3. The slower response also means that the output is not following the audio wave very well, so it cannot reproduce the audo wave very accurately (ie is distorted) even if you can filter out the artifact noise.
In almost all cases the other algorithms will give better playback performance. However for some cases wehere you are limited to one PIC digital output pin at some bitrates algorithm 1.1 might slightly outperform the basic algorithm 1.0.
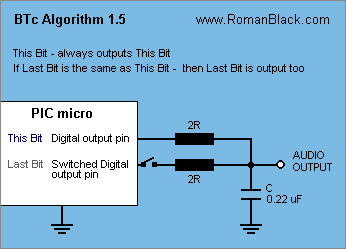
Algorithm BTc 1.5
My good old algorithm 1.5 was included in my work in 2001 and still remains one of the two best algorithms for sound playback quality.
Playback.
It requires 2 digital output pins, and one pin is required to be able to go high-impedance (disconnect). There are 2 equal value resistors, each from a pin to the capacitor. One pin always outputs the new bit to the cap. The other pin outputs the previous (last) bit, but only if it matches the new bit. If the bits are different only the new bit is output. The resistor values are each 2*R.
The result is that the cap voltage moves the correct BTc distance (ie 1/8 of the distance if using BTc8) when the 2 bits match. But if the new bit is different to the last bit the new bit only moves the cap HALF of that distance. In effect this halves the amplitude of the noise artifacts while still allowing fast response to provide good tracking of the audio wave and low distortion.
a1.5 Encoding Example (using BTc8);
variables; NewSample = the new audio sample, scaled to 1/4-3/4 Vcc range LastVoltage = the cap voltage (audio output) from the last bit NewVoltage = the cap voltage (audio output) after we encode this new bit LastBit = the encoded bit from last time NewBit = the newly encoded BTc bit encoding; 1. if LastBit was 1; (we can move up 1/8 or move down 1/16) generate a 1bit; distance = (Vcc - LastVoltage) / 8 Voltage1 = LastVoltage + distance generate a 0bit; distance = (LastVoltage - Gnd) / 16 Voltage0 = LastVoltage - distance 2. if LastBit was 0; (we can move down 1/8 or move up 1/16) generate a 1bit; distance = (Vcc - LastVoltage) / 16 Voltage1 = LastVoltage + distance generate a 0bit; distance = (LastVoltage - Gnd) / 8 Voltage0 = LastVoltage - distance 3. Find which bit is closest to the desired audio sample; if Voltage1 is closest to NewSample then; NewBit =1, and NewVoltage = Voltage1 if Voltage0 is closest to NewSample then; NewBit =0, and NewVoltage = Voltage0 4. Save the cap voltage and repeat for the next audio sample; LastVoltage = NewVoltage Repeat
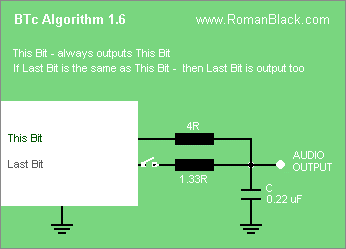
Algorithm BTc 1.6 (new for BTc Encoder v3.0)
This is a subtle variation of my 1.5 algorithm. I developed and refined this in early 2009 to allow the very best sound playback when using lower bitrates, ie up to 44kHz.
Playback.
Is almost identical to algorithm 1.5, in fact it uses the same playback software. The difference is only in the value of the 2 output resistors.
It requires 2 digital output pins, and one pin is required to be able to go high-impedance (disconnect). There are 2 resistors, each from a pin to the capacitor;
New Bit Pin -> resistor value 4R -> is always output
Last Bit Pin -> resistor value 1.33R -> is output only when the bits match
One pin always outputs the new bit to the cap. The other pin outputs the previous (last) bit, but only if it matches the new bit. If the bits are different only the new bit is output. The result is that the cap voltage moves the correct BTc distance (ie 1/8 of the distance if using BTc8) when the 2 bits match. But if the new bit is different to the last bit the new bit only moves the cap ONE QUARTER of that distance. In effect this reduces the amplitude of the noise artifacts by 4, while still allowing fast(ish) response to provide good tracking of the audio wave and low distortion.
a1.6 Encoding Example (using BTc8);
(note is almost identical to algorithm 1.5)
variables; NewSample = the new audio sample, scaled to 1/4-3/4 Vcc range LastVoltage = the cap voltage (audio output) from the last bit NewVoltage = the cap voltage (audio output) after we encode this new bit LastBit = the encoded bit from last time NewBit = the newly encoded BTc bit encoding; 1. if LastBit was 1; (we can move up 1/8 or move down 1/32) generate a 1bit; distance = (Vcc - LastVoltage) / 8 Voltage1 = LastVoltage + distance generate a 0bit; distance = (LastVoltage - Gnd) / 32 Voltage0 = LastVoltage - distance 2. if LastBit was 0; (we can move down 1/8 or move up 1/32) generate a 1bit; distance = (Vcc - LastVoltage) / 32 Voltage1 = LastVoltage + distance generate a 0bit; distance = (LastVoltage - Gnd) / 8 Voltage0 = LastVoltage - distance 3. Find which bit is closest to the desired audio sample; if Voltage1 is closest to NewSample then; NewBit =1, and NewVoltage = Voltage1 if Voltage0 is closest to NewSample then; NewBit =0, and NewVoltage = Voltage0 4. Save the cap voltage and repeat for the next audio sample; LastVoltage = NewVoltage Repeat
Algorithm BTc 1.7 (new for BTc Encoder v3.0)
This is like a "poor cousin" to the a1.5 and a1.6 algorithms. It does not perform as good. However is is generally better than the a1.0 and a1.1 algorithms. I did some work on this algorithm in years previously but never included it as it could never match the performance of my a1.5.
However people have asked me for a playback algorithm that gives better sound than 1 digital output pin, but does NOT require turning a digital output pin to high impedance state. Some of the cheapest microprocessors do not have this ability and there may be some cases where the user does not want to constantly be changing a digital pin from output->high impedance. This is the only advantage of a1.7, so if you can change an output pin to/from high impedance state (as with most microprocessors) you will get much better performance from a1.5 and a1.6.
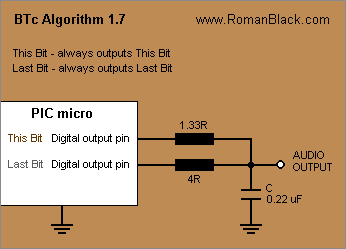
Playback.
Is very straightforward, there are 2 digital output pins and 2 resistors going to the capacitor;
New Bit Pin -> resistor value 1.33R -> is always output
Last Bit Pin -> resistor value 4R -> is always output
The result is a little complex; when the 2 bits match, the cap voltage moves the standard BTc distance (ie 1/8 for BTc8) towards Vcc or Gnd. However, when the bits do not match the 2 different resistor values form a voltage divider network;
Last Bit = 0, New Bit = 1; cap voltage is pulled the BTc distance towards a destination; 3/4 Vcc
Last Bit = 1, New Bit = 0; cap voltage is pulled the BTc distance towards a destination; 1/4 Vcc
Fortunately this is still quite easy and fast to BTc encode;
a1.7 Encoding Example (using BTc8);
variables; NewSample = the new audio sample, scaled to 1/4-3/4 Vcc range LastVoltage = the cap voltage (audio output) from the last bit NewVoltage = the cap voltage (audio output) after we encode this new bit LastBit = the encoded bit from last time NewBit = the newly encoded BTc bit encoding; 1. if LastBit was 1; (we can move up 1/8, or move down 1/8 towards destination 1/4Vcc) generate a 1bit; distance = (Vcc - LastVoltage) / 8 Voltage1 = LastVoltage + distance generate a 0bit; distance = (LastVoltage - 1/4Vcc) / 8 Voltage0 = LastVoltage - distance 2. if LastBit was 0; (we can move down 1/8, or move up 1/8 towards destination 3/4Vcc) generate a 1bit; distance = (3/4Vcc - LastVoltage) / 8 Voltage1 = LastVoltage + distance generate a 0bit; distance = (LastVoltage - Gnd) / 8 Voltage0 = LastVoltage - distance 3. Find which bit is closest to the desired audio sample; if Voltage1 is closest to NewSample then; NewBit =1, and NewVoltage = Voltage1 if Voltage0 is closest to NewSample then; NewBit =0, and NewVoltage = Voltage0 4. Save the cap voltage and repeat for the next audio sample; LastVoltage = NewVoltage Repeat
I have refined this (by testing different resistor values) to be about the best it can be. As the resistor ratio increases above the 1:3 ratio I recommend (1.33R : 4R), the algorithm starts to approach the performance of a1.0 with all its characteristics including faster response but larger noise artifacts. If the resistors are adjusted closer to the ratio 1:1 values of the failed algorithm (see below) its performace starts to approach the very poor performance of the failed algorithm. The best middle ground is right around the 1:3 ratio I have chosen, which just happens to be a binary voltage divider (1/4Vcc and 3/4Vcc) which suits fast and easy BTc encoding.
Why is a1.7 not as good as a1.5 and a1.6?
On the Sound Encoder screen these 3 algorithms produce encoded waves that don't LOOK too different. This is true when the sound wave is low in volume (near the centre region of the screen). However there is an important difference as the sound wave volume increases (near the top and bottom of the screen) the 1.7 algorithm starts to overcompensate and produces a nasty repeating artifact typically at bitrate/4 and bitrate/5 which is hard to filter and at a low enough freq to be very audible. In comparison with the same audio wave the a1.5 and a1.6 algorithms will produce some bitrate/4 and bitrate/5 artifacts, but at much lower amplitude and much more random, and will be mixed amongst bitrate/2 and bitrate/3 artifacts which are much higher freq and easier to filter. So use the a1.5 and a1.6 algorithms wherever possible.
The failed algorithm!
I will mention this as people keep asking me about it. Like the a1.1 algorithm it is simple to imagine and on first thought people think this will work well. I didn't include it in 2001 as it performs so badly and I am only covering it here so people stop emailing me suggesting this algorithm! :)
Playback.
There are 2 output pins and 2 equal value resistors. One pin always outputs the new bit, the other pin always outputs the last bit.
On first thought this sounds good; when the 2 bits are different the cap voltage will be pulled towards the middle (1/2Vcc) and when the bits are the same it will make a BTc move towards Vcc or Gnd as usual. During silent parts of the audio wavform the 01010101 bitstream will produce a silent output. Or that's what people think...
In reality the audio waveform does not remain exactly in the centre during quiet passages. It is a gentle slope NEAR the centre. In this case this algorithm is terrible, it does nothing for a period maybe bitrate/5 to bitrate/20, then makes a nasty overcorrection and repeats. The result is that it makes a very unpleasant low freq (that you can't filter out) loud "whine" all through the quieter parts of the sound. Additionally near the louder parts of the sound it overcorrects in a repetitive fashion at about bitrate/4 similar (but worse) to algorithm 1.7. There is no good side, this algorithm performs much worse than any others here and I have never included it as an option in my BTc Sound Encoder software.
Which is the BEST algorithm?
The reason I have included the above five algorithms in BTc Sound Encoder is because it depends on the actual wave sound and bitrate that you want to reproduce. It can also depend on what hardware limitations you may have in your playback hardware since the main use for BTc sound is adding sound to CHEAP hardware.
Generally the new algorithm 1.6 is the best, for lowish bitrates of up to about 40kHz. Use this one. The reason it is better than a1.5 at lower bitrates is because at lower bitrates the main thing that sounds bad are the noise artifacts. With a1.6 these artifacts are only 1/4 the amplitude of single bit playback like a1.0. Algorithm 1.6 also has the best "randomisation" of the noise artifacts so artifacts at bitrate/2 /3 /4 etc will be randomly mixed which is easier for the human ear to ignore than a fixed freq artifact. These artifacts are also as high a freq as possible, with most being bitrate/2 and bitrate/3 which are high enough to either be above human hearing or at least high enough for good filter effectiveness.
For bitrates 30kHz to 80kHz algorithm 1.5 is the best. Although a1.5 has double the noise artifact amplitude of a1.6 and the artifacts are a little less random, this is less critical at you approach 80kHz as most of the bitrate/2 /3 /4 artifacts are above human hearing and will filter out very easily. With the noise artifacts more easily removed the main issue becomes the ability to accurately track and reproduce the audio waveform, and a1.5 can respond slightly faster than a1.6 and with slightly less overshoot, so it more accurately tracks the audio wave and gives lower distortion. So if your bitrate is high enough where PCM noise is not really a problem, or if you are using good hardware filtering then a1.5 is the best.
For very high bitrates 50kHz up to 200kHz algorithm 1.0 is the best! Yes, the simple algorithm 1.0 which is just changing a digital output pin! At these very high bitrates the noise artifacts are a high freq almost certainly well above human hearing and your filter will take them out, even those spiky looking bitrate/2 /3 /4 artifacts which are all over a a1.0 waveform. The only factor then is to accurately track the audio wave and the 1.0 algorithm is the fastest responding and has the least overshoot. An additional benefit is that at very high bitrates this takes less processing time in your playback firmware as you only need to test 1bit and operate 1 digital output pin and do not need to make any pins high-impedance.
With limited hardware. If you have 2 digital output pins but do not have the ability to change one pin to high-impedance then the best algorithm is 1.7. This gives smaller amplitude and more random noise artifacts than a1.0 and is well worth the cost of the extra pin and resistor, provided of course that you can't do a1.5 or a1.6.
Encoding factors
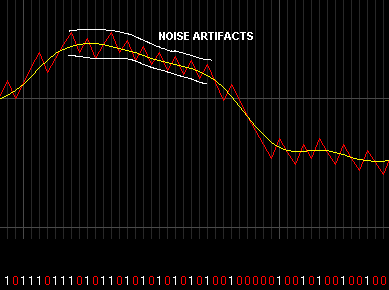
Noise artifacts
This is a problem where the BTc encoded sound still follows the average of the original sound, BUT there is a high frequency noise (the spikes) on the encoded waveform. This is generally heard as a "whine" or "fizz" over the top of the sound. This problem always exists with 1bit sound due to the simple nature of the sound generation so the best you can do is reduce these where possible. When encoding try to reduce the noice artifacts by using higher bitrates, higher BTc fineness values, and a high BTc Algorithm. Generally BTc alg 1.6 reduces these artifacts the best.
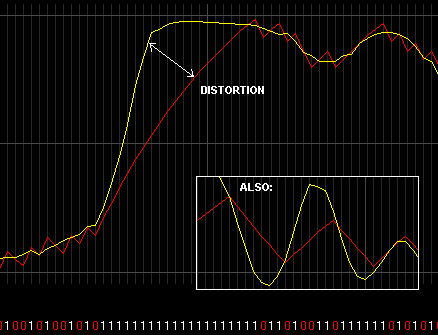
Distortion
This is a separate problem when encoding. Distortion is a situation where the BTc encoded waveform cannot respond fast enough to reproduce the original waveform. Distortion of this type is generally heard as a "harshness" "clickyness" of the sound on loud passages. Distortion is caused by the opposite of the factors that cause the noise artifacts. To reduce the distortion, use lower BTc fineness values, and a lower BTc algorithm. Generally BTc alg 1.0 has the least distortion.
The balancing act!
Getting good sound encoding and playback requires constantly balancing these two sound problems. In most cases you want to adjust the encoding to reduce the noise artifacts even if you must live with some distorion. At high bitrates a lot of the noise artifacts will be above human hearing (or above the hardware filter cutoff), so you will get better sound by reducing the distortion and increasing the noise artifacts. But at low bitrates you often get the best sound by increasing distortion and reducing the noise artifacts "whine".
Fortunately BTc Sound Encoder v3.0 has a lot of encoding options and you can see instantly on the screen the results of encoding so it is easy to find a decent "balance" of encoding parameters.
Examples of good encoding
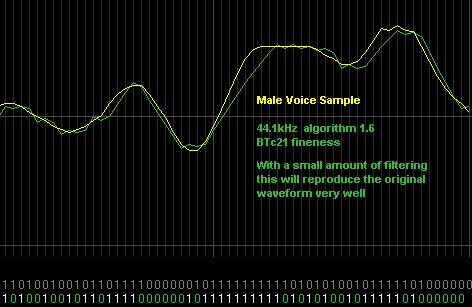
Above shows voice at 44.1kHz which can be reproduced quite well using BTC alg 1.6. This shows a touch of distortion, and nicely reduced noise artifacts. With just a little hardware filtering the result is fairly clear sounding speech with only a touch of "fizz".

Above shows voice at 88.2kHz using BTc alg 1.5 here you can see the distortion has been completely dialed out, leaving just noise artifacts. The BTc waveform follows the original sound quite accurately (on average). The noise artifacts worst case is a repeated string of 0001, bitrate/4 which is 22kHz. Most of the noise artifacts are at /3 (29kHz) or /2 (44kHz) and are very easy to filter out. The result to the ear is close to CD quality audio.
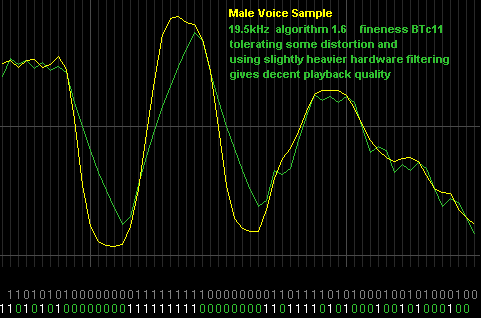
Voice at 19.5kHz (above) is more of a challenge. Using BTc alg 1.6 (as it has the lowest noise artifacts) and a lower BTc fineness of 11, to give faster response and less ditortion. The best resulting sound came from tolerating a fair amount of distortion in order to keep the noise artifacts as low as possible. The noise artifacts are mainly bitrate /2 /3 /4. At 19.5kHz bitrate these are quite low noise frequencies of 9.7kHz, 6.5kHz and 4.8kHz which are loud to the ear so a fairly heavy hardware filter was used at about 5kHz. The sound of the voice was gritty and fizzy but was still fully understandable and suitable for simple applications.
The one thing that always applies with 1bit sound is that the higher the bitrate, the better it sounds and the easier it is to dial in good encoding parameters. In the 8 years since I released the BTc PICsound project memory prices have dropped so much, the best advice I can give is just to buy a nice big 512kbit or 1Mbit eeprom for a couple of dollars and use a high bitrate like 39.062kHz, 44.1kHz or 78.124kHz.
History pictures
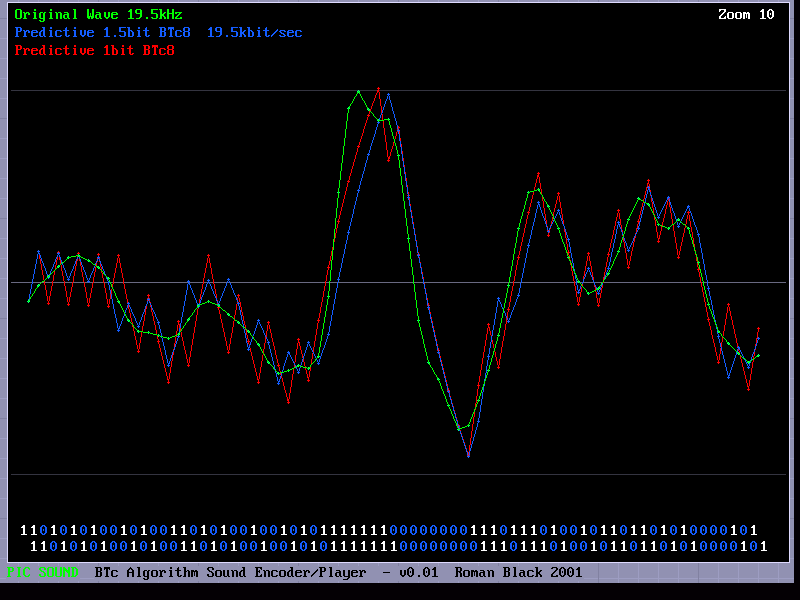
Nostalgia! - A screenshot of the first BTc Encoder I publicly released, (dos version 0.01).
- end -
[Back to Home Page]